菱形ABCD的对角线AC,BD相交于点O, .动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为
.动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为 ,未盖住部分的面积为
,未盖住部分的面积为 ,
,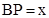 .
.
(1)用含x代数式分别表示 ,
, ;
;
(2)若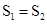 ,求x.
,求x.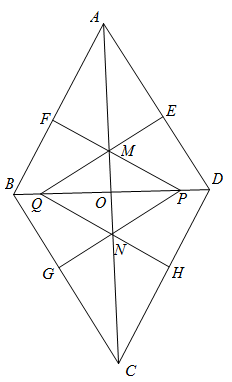
推荐套卷
菱形ABCD的对角线AC,BD相交于点O, .动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为
.动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为 ,未盖住部分的面积为
,未盖住部分的面积为 ,
,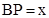 .
.
(1)用含x代数式分别表示 ,
, ;
;
(2)若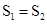 ,求x.
,求x.