已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线C:x2=2py(p>0)上运动,MN为圆O′在x轴上所截得的弦.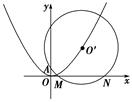
(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.
相关知识点
推荐套卷
已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线C:x2=2py(p>0)上运动,MN为圆O′在x轴上所截得的弦.
(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.