对于三次函数 ,定义
,定义 是
是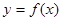 的导函数
的导函数 的导函数,若方程
的导函数,若方程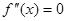 有实数解
有实数解 ,则称点
,则称点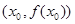 为函数
为函数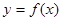 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数 都关于点
都关于点 对称:
对称:
②存在三次函数 ,若
,若 有实数解
有实数解 ,则点
,则点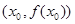 为函数
为函数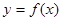 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则:
,则: 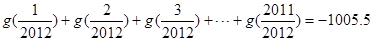
其中所有正确结论的序号是( ).
| A.①②④ | B.①②③ | C.①③④ | D.②③④ |
推荐套卷
对于三次函数 ,定义
,定义 是
是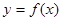 的导函数
的导函数 的导函数,若方程
的导函数,若方程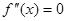 有实数解
有实数解 ,则称点
,则称点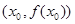 为函数
为函数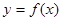 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数 都关于点
都关于点 对称:
对称:
②存在三次函数 ,若
,若 有实数解
有实数解 ,则点
,则点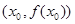 为函数
为函数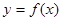 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则:
,则: 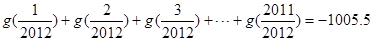
其中所有正确结论的序号是( ).
| A.①②④ | B.①②③ | C.①③④ | D.②③④ |