已知点C(1,0)，点A、B是⊙O：x2＋y2＝9上任意两个不同的点，且满足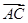
·
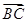＝0，设P为弦AB的中点．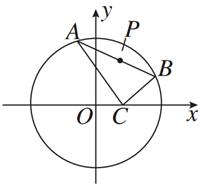
(1)求点P的轨迹T的方程；
(2)试探究在轨迹T上是否存在这样的点：它到直线x＝－1的距离恰好等于到点C的距离？若存在，求出这样的点的坐标；若不存在，说明理由．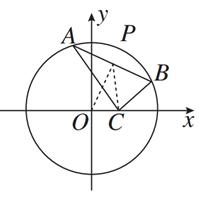
相关试题
，其中
为正实数．
是函数
的极值点，讨论函数
的单调性；
上无最小值，且
在
，动圆
过点
且与圆
相切，记圆心
．
在
与
关于原点对称，且
，当
的面积最小时，求直线
的方程．
的底面为菱形，
，
，
．
；
中，
，
为
．
，求
；
，求
．
套餐，对国庆节当日办理套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元，国庆节当天参与活动的人数统计结果如图所示，现将频率视为概率．
相关知识点
推荐套卷
已知点C(1,0)，点A、B是⊙O：x2＋y2＝9上任意两个不同的点，且满足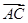·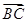＝0，设P为弦AB的中点．
(1)求点P的轨迹T的方程；
(2)试探究在轨迹T上是否存在这样的点：它到直线x＝－1的距离恰好等于到点C的距离？若存在，求出这样的点的坐标；若不存在，说明理由．
粤公网安备 44130202000953号