已知顶点在坐标原点，焦点在x轴正半轴的抛物线上有一点A(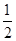
，m)，A点到抛物线焦点的距离为1．
(1)求该抛物线的方程；
(2)设M(x0，y0)为抛物线上的一个定点，过M作抛物线的两条互相垂直的弦MP，MQ，求证：PQ恒过定点(x0＋2，－y0)．
相关知识点
推荐套卷
已知顶点在坐标原点，焦点在x轴正半轴的抛物线上有一点A(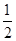，m)，A点到抛物线焦点的距离为1．
(1)求该抛物线的方程；
(2)设M(x0，y0)为抛物线上的一个定点，过M作抛物线的两条互相垂直的弦MP，MQ，求证：PQ恒过定点(x0＋2，－y0)．
粤公网安备 44130202000953号