设圆C与两圆(x＋
)2＋y2＝4，(x－)2＋y2＝4中的一个内切，另一个外切．
(1)求C的圆心轨迹L的方程；
(2)已知点M(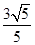
，
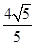)，F(，0)，且P为L上动点，求||MP|－|FP||的最大值及此时点P的坐标．
相关试题
的两根
满足
，且
表示
;（2）求证：数列
是等比数列;
的前n项和
.
的前
项和为
，
，
．求数列
}的前n 项和为
，已知
,
,
成等差数列
－
＝3，求
，试判断函数
在（0，+∞）上的单调性，并加以证明。相关知识点
推荐套卷
设圆C与两圆(x＋)2＋y2＝4，(x－)2＋y2＝4中的一个内切，另一个外切．
(1)求C的圆心轨迹L的方程；
(2)已知点M(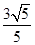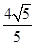，)，F(，0)，且P为L上动点，求||MP|－|FP||的最大值及此时点P的坐标．
粤公网安备 44130202000953号