在△ABC中，∠A，∠B，∠C所对的边分别是a、b、c，不等式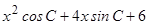
≥0对一切实数
恒成立.
（1）求cosC的取值范围；
（2）当∠C取最大值，且△ABC的周长为6时，求△ABC面积的最大值，并指出面积取最大值时△ABC的形状.
相关试题
，一个焦点是F（0，1）．
过点F交椭圆于A、B两点，且
，求直线
时,求函数
的最小值;
,
恒成立,试求实数
的取值范围.
，
的等比中项。
是等差数列；
的前n项和为Tn,求Tn。
图象的对称中心的横坐标；
，求函数
的定义域为集合A,函数
的定义域为集合B.
A，求实数
的取值范围。推荐套卷
在△ABC中，∠A，∠B，∠C所对的边分别是a、b、c，不等式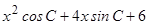≥0对一切实数恒成立.
（1）求cosC的取值范围；
（2）当∠C取最大值，且△ABC的周长为6时，求△ABC面积的最大值，并指出面积取最大值时△ABC的形状.
粤公网安备 44130202000953号