甲有一只放有x个红球,y个黄球,z个白球的箱子,乙有一只放有3个红球,2个黄球,1个白球的箱子,
(1)两个各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜。若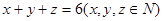 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;
(2)在(1)下又规定当甲取红、黄、白球而胜的得分分别为1、2、3分,否则得0分,求甲得分的期望的最大值及此时x、y、z的值。
相关知识点
推荐套卷
甲有一只放有x个红球,y个黄球,z个白球的箱子,乙有一只放有3个红球,2个黄球,1个白球的箱子,
(1)两个各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜。若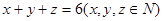 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;
(2)在(1)下又规定当甲取红、黄、白球而胜的得分分别为1、2、3分,否则得0分,求甲得分的期望的最大值及此时x、y、z的值。