如图,已知抛物线,过点任作一直线与相交于两点,过点作轴的平行线与直线相交于点(为坐标原点).
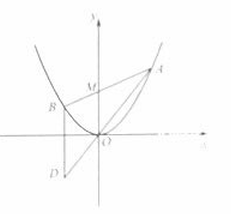
(1)证明:动点在定直线上;
(2)作的任意一条切线(不含轴)与直线相交于点,与(1)中的定直线相交于点,证明:为定值,并求此定值.
相关知识点
推荐套卷
如图,已知抛物线,过点任作一直线与相交于两点,过点作轴的平行线与直线相交于点(为坐标原点).

(1)证明:动点在定直线上;
(2)作的任意一条切线(不含轴)与直线相交于点,与(1)中的定直线相交于点,证明:为定值,并求此定值.