已知双曲线的两条渐近线分别为.
(1)求双曲线的离心率;
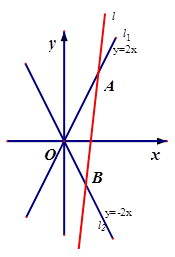
(2)如图,为坐标原点,动直线分别交直线于两点(分别在第一,四象限),且的面积恒为8,试探究:是否存在总与直线有且只有一个公共点的双曲线?若存在,求出双曲线的方程;若不存在,说明理由.
相关知识点
推荐套卷
已知双曲线的两条渐近线分别为.

(1)求双曲线的离心率;
(2)如图,为坐标原点,动直线分别交直线于两点(分别在第一,四象限),且的面积恒为8,试探究:是否存在总与直线有且只有一个公共点的双曲线?若存在,求出双曲线的方程;若不存在,说明理由.