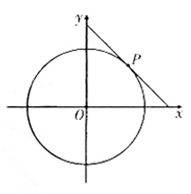
圆的切线与轴正半轴,轴正半轴围成一个三角形,当该三角形面积最小时,切点为(如图),双曲线过点且离心率为.
(1)求的方程;
(2)椭圆过点P且与有相同的焦点,直线过的右焦点且与交于两点,若以线段为直径的圆心过点,求的方程.
推荐套卷
圆的切线与轴正半轴,轴正半轴围成一个三角形,当该三角形面积最小时,切点为(如图),双曲线过点且离心率为.
(1)求的方程;
(2)椭圆过点P且与有相同的焦点,直线过的右焦点且与交于两点,若以线段为直径的圆心过点,求的方程.
