已知等差数列{an}的首项a1＝1，公差d>0，且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项．
(1)求数列{an}，{bn}的通项公式；
(2)设数列{cn}对n∈N*，均有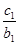
＋
＋…＋
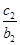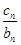＝an＋1成立，求c1＋c2＋c3＋…＋c2014的值．
相关试题
为偶函数，且
的最小值是
.
；
.
的最小值；
，求
的值.
.
的奇偶性；
=
，其中
，
．
，
，
，…，
成等差数列，且
，公差
，求证：
；
，
，记
，且不等式
对于
恒成立，求实数
的取值范围．
表示
的整数部分，如：
，设
为随机变量，
．
；
．相关知识点
推荐套卷
已知等差数列{an}的首项a1＝1，公差d>0，且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项．
(1)求数列{an}，{bn}的通项公式；
(2)设数列{cn}对n∈N*，均有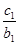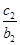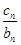＋＋…＋＝an＋1成立，求c1＋c2＋c3＋…＋c2014的值．
粤公网安备 44130202000953号