某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
相关知识点
推荐套卷

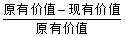 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计) 的身高,单位:cm),分组情况如下:
的身高,单位:cm),分组情况如下:

 65.5
65.5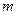


 ,
,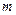 的值,并画出频率分布直方图;
的值,并画出频率分布直方图;
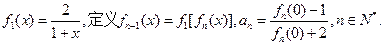
 的递推关系式,并求出
的递推关系式,并求出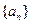 的通项公式;
的通项公式;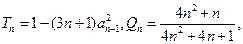 试比较
试比较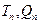 大小
大小 并证明
并证明 ,函数
,函数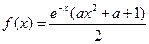 ,其中e是自然对数的底数。
,其中e是自然对数的底数。 在[-1,2]上的最小值;
在[-1,2]上的最小值; 是否存在实数t,使得对于任意
是否存在实数t,使得对于任意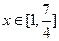 ,
, 恒成立,存在,求出t的范围,不存在,说明理由。
恒成立,存在,求出t的范围,不存在,说明理由。
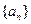 的通项公式;
的通项公式; 求数列
求数列 的前n项和
的前n项和
 粤公网安备 44130202000953号
粤公网安备 44130202000953号