如图,已知二次函数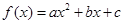 的图像过点
的图像过点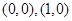 和
和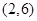 ,直线
,直线 ,直线
,直线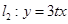 (其中
(其中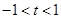 ,
,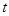 为常数);若直线
为常数);若直线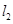 与函数
与函数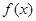 的图像以及直线
的图像以及直线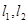 与函数
与函数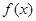 以及的图像所围成的封闭图形如阴影所示.
以及的图像所围成的封闭图形如阴影所示.
(1)求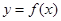 ;
;
(2)求阴影面积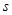 关于
关于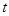 的函数
的函数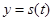 的解析式;
的解析式;
(3)若过点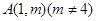 可作曲线
可作曲线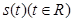 的三条切线,求实数
的三条切线,求实数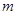 的取值范围.
的取值范围.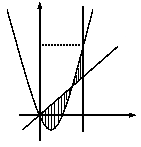
相关知识点
推荐套卷
如图,已知二次函数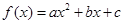 的图像过点
的图像过点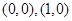 和
和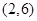 ,直线
,直线 ,直线
,直线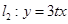 (其中
(其中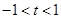 ,
,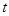 为常数);若直线
为常数);若直线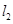 与函数
与函数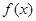 的图像以及直线
的图像以及直线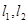 与函数
与函数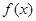 以及的图像所围成的封闭图形如阴影所示.
以及的图像所围成的封闭图形如阴影所示.
(1)求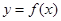 ;
;
(2)求阴影面积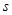 关于
关于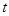 的函数
的函数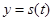 的解析式;
的解析式;
(3)若过点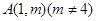 可作曲线
可作曲线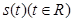 的三条切线,求实数
的三条切线,求实数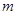 的取值范围.
的取值范围.