已知椭圆G：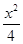
＋y2＝1.过
轴上的动点
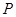(m,0)作圆x2＋y2＝1的切线l交椭圆G于A，B两点．
（1）求椭圆G上的点到直线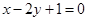
的最大距离;
（2）①当实数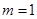
时,求A，B两点坐标;
②将|AB|表示为m的函数，并求|AB|的最大值．
相关试题
的方程
的两根分别在区间
与
内，求
的取值范围．
的不等式
.
的前n项和为
，且
、
；
，问数列
的前多少项的和最小？最小值是多少？
且
.
求△ABC的面积.
（0，
），椭圆
：
的离心率为
，
是椭圆的焦点，直线
的斜率为
，
为坐标原点．
与
两点，当
的面积最大时，求
的方程．相关知识点
推荐套卷
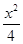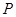已知椭圆G：＋y2＝1.过轴上的动点(m,0)作圆x2＋y2＝1的切线l交椭圆G于A，B两点．
（1）求椭圆G上的点到直线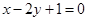的最大距离;
（2）①当实数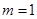时,求A，B两点坐标;
②将|AB|表示为m的函数，并求|AB|的最大值．
粤公网安备 44130202000953号