已知函数f(x)=ax-ln x,g(x)= ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
(1)当a=1时,求函数f(x)的最小值;
(2)当a=1时,求证:f(m)>g(n)+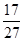 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立;
(3)是否存在实数a,使得f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由.
推荐套卷
已知函数f(x)=ax-ln x,g(x)= ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
(1)当a=1时,求函数f(x)的最小值;
(2)当a=1时,求证:f(m)>g(n)+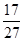 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立;
(3)是否存在实数a,使得f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由.