如图，在四棱锥E﹣ABCD中，矩形ABCD所在的平面与平面AEB垂直，且∠BAE=120°，AE=AB=4，AD=2，F，G，H分别为BE，AE，BC的中点
（1）求证：DE∥平面FGH；
（2）若点P在直线GF上，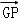
=λ
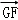，且二面角D﹣BP﹣A的大小为
，求λ的值．
相关试题
．
时，求
在区间
上的最大值；
上，函数
下方，求
的取值范围．
：函数
的值域为
；命题
：不等式
对一切
均成立．如果命题“
”为真命题，且“
”为假命题，求实数
的取值范围．
，底面三角形
为正三角形，侧棱
底面
，
，
为
的中点，
为
中点．
平面
；
到平面
满足：
，
．设
为数列
的前
项和，已知
，
，
，求数列
的前
．
中，角
所对的边分别为
，且满足
，
．
，求
的值．相关知识点
推荐套卷
如图，在四棱锥E﹣ABCD中，矩形ABCD所在的平面与平面AEB垂直，且∠BAE=120°，AE=AB=4，AD=2，F，G，H分别为BE，AE，BC的中点
（1）求证：DE∥平面FGH；
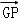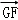（2）若点P在直线GF上，=λ，且二面角D﹣BP﹣A的大小为，求λ的值．
粤公网安备 44130202000953号