如图,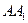 ,
,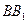 为圆柱
为圆柱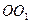 的母线,
的母线,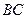 是底面圆
是底面圆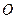 的直径,
的直径,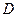 ,
,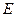 分别是
分别是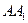 ,
, 的中点,
的中点,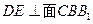 .
.
(1)证明: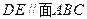 ;
;
(2)证明: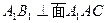 ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥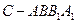 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.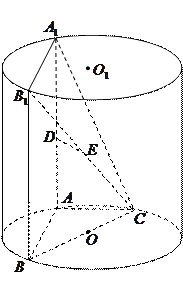
推荐套卷
如图,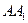 ,
,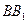 为圆柱
为圆柱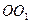 的母线,
的母线,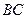 是底面圆
是底面圆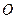 的直径,
的直径,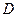 ,
,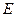 分别是
分别是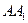 ,
, 的中点,
的中点,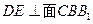 .
.
(1)证明: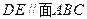 ;
;
(2)证明: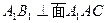 ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥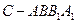 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.