边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1)，现将正方形ABCD绕D点顺时针旋转，当A点第一次落在DF上时停止旋转，旋转过程中， AB边交DF于点M，BC边交DG于点N.
（1）求边DA在旋转过程中所扫过的面积；
（2）旋转过程中，当MN和AC平行时(如图2)，求正方形ABCD旋转的度数；
（3）如图3，设△MBN的周长为p，在旋转正方形ABCD的过程中，p值是否有变化？请证明你的结论.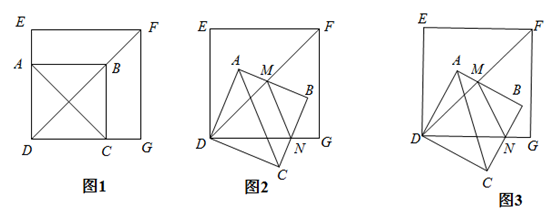
相关试题
如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．
⑴求证：CE＝CF；
⑵若G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？
推荐套卷
粤公网安备 44130202000953号