如图，在矩形ABCD中，AB=16cm，AD=6cm，动点P、Q分别从A、C同时出发，点P以每秒3cm的速度向B移动，一直达到B止，点Q以每秒2cm的速度向D移动．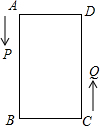
（1）P、Q两点出发后多少秒时，四边形PBCQ的面积为36cm2；
（2）是否存在某一时刻，使PBCQ为正方形？
相关试题
相关知识点
推荐套卷
如图，在矩形ABCD中，AB=16cm，AD=6cm，动点P、Q分别从A、C同时出发，点P以每秒3cm的速度向B移动，一直达到B止，点Q以每秒2cm的速度向D移动．
（1）P、Q两点出发后多少秒时，四边形PBCQ的面积为36cm2；
（2）是否存在某一时刻，使PBCQ为正方形？
粤公网安备 44130202000953号