某地区一种商品的需求量
（万件）、供应量
（万件）与价格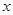
（元／件）分别近似满足下列函数关系式：
，
．需求量为0时，即停止供应．当
时，该商品的价格称为稳定价格，需求量称为稳定需求量．
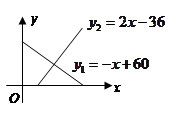
（1）求该商品的稳定价格与稳定需求量；
（2）价格在什么范围，该商品的需求量低于供应量？
（3）当需求量高于供应量时，政府常通过对供应方提供价格补贴来提高供货价格，以提高供应量．现若要使稳定需求量增加4万件，政府应对每件商品提供多少元补贴，才能使供应量等于需求量？
相关试题
（河池）如图，AB为⊙O的直径，CO⊥AB于O，D在⊙O上，连接BD，CD，延长CD与AB的延长线交于E，F在BE上，且FD=FE．
（1）求证：FD是⊙O的切线；
（2）若AF=8，tan∠BDF=
，求EF的长．
（河池）如图，在△ABC中，∠ACB=90°，AC=BC=AD．
（1）作∠A的平分线交CD于E；
（2）过B作CD的垂线，垂足为F；
（3）请写出图中两对全等三角形（不添加任何字母），并选择其中一对加以证明．
．（桂林）如图，四边形ABCD是⊙O的内接正方形，AB=4，PC、PD是⊙O的两条切线，C、D为切点．
（1）如图1，求⊙O的半径；
（2）如图1，若点E是BC的中点，连接PE，求PE的长度；
（3）如图2，若点M是BC边上任意一点（不含B、C），以点M为直角顶点，在BC的上方作∠AMN=90°，交直线CP于点N，求证：AM=MN．
相关知识点
推荐套卷
粤公网安备 44130202000953号