某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组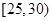 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组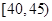 ,第5组
,第5组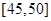 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
推荐套卷
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组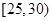 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组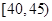 ,第5组
,第5组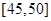 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。