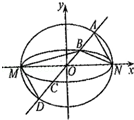
如图,已知椭圆与的中心在坐标原点,长轴均为且在轴上,短轴长分别为,,过原点且不与轴重合的直线与的四个交点按纵坐标从大到小依次为,记,和的面积分别为和.
(1)当直线与轴重合时,若,求的值;
(2)当变化时,是否存在与坐标轴不重合的直线,使得?并说明理由.
相关知识点
推荐套卷
如图,已知椭圆与的中心在坐标原点,长轴均为且在轴上,短轴长分别为,,过原点且不与轴重合的直线与的四个交点按纵坐标从大到小依次为,记,和的面积分别为和.
(1)当直线与轴重合时,若,求的值;
(2)当变化时,是否存在与坐标轴不重合的直线,使得?并说明理由.
