某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间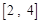 的有8人.
的有8人.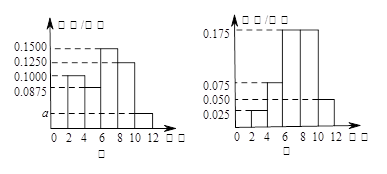
(1)求直方图中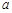 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间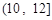 的人数;
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为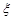 ,求
,求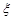 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间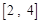 的有8人.
的有8人.
(1)求直方图中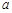 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间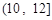 的人数;
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为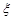 ,求
,求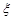 的分布列和数学期望.
的分布列和数学期望.