已知a，b是不相等的正数，在a，b之间分别插入m个正数a1，a2， ，am和正数b1，b2， ，
bm，使a，a1，a2， ，am，b是等差数列，a，b1，b2， ，bm，b是等比数列．
（1）若m＝5，
＝
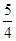，求
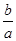的值；
（2）若b＝λa(λ∈N*，λ≥2)，如果存在n (n∈N*，6≤n≤m)使得an－5＝bn，求λ的最小值及此时m的值；
（3）求证：an＞bn(n∈N*，n≤m)．
相关试题
，
。
的最小正周期和单调递减区间；
上的最小值和最大值，并求出取得最值时
的值。
，
，
时，求
的子集的个数；
且
时，求
的取值范围。
中，
面
，
是直角三角形，
，
，
，点
分别为
的中点。
；
与平面
所成的角的大小；
的正切值。
轴的两个直角坐标平面
和
所成的二面角
等于
.已知
的方程是
，求曲线
中，
底面
，
，
,
,点
，
分别在棱
上，且
平面
；
的中点时，求
与平面
为直二面角？并说明理由.推荐套卷
已知a，b是不相等的正数，在a，b之间分别插入m个正数a1，a2， ，am和正数b1，b2， ，
bm，使a，a1，a2， ，am，b是等差数列，a，b1，b2， ，bm，b是等比数列．
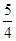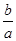（1）若m＝5，＝，求的值；
（2）若b＝λa(λ∈N*，λ≥2)，如果存在n (n∈N*，6≤n≤m)使得an－5＝bn，求λ的最小值及此时m的值；
（3）求证：an＞bn(n∈N*，n≤m)．
粤公网安备 44130202000953号