正方形ABCD中,点O是对角线DB的中点,点P在DB所在的直线上,PE⊥BC于E,PF⊥DC于F.
(1)如图1,当点P与点O重合时,延长FP交AB于点M,求证:AP=EF;
(2)如图2,当点P在线段DB上(不与点D、O、B重合)时,延长FP交AB于点M,求证:AP=EF;
(3)如图3,当点P在DB的延长线上时,请你猜想AP与EF的数量关系及位置关系,直接写出结论;若不成立,请写出相应的结论.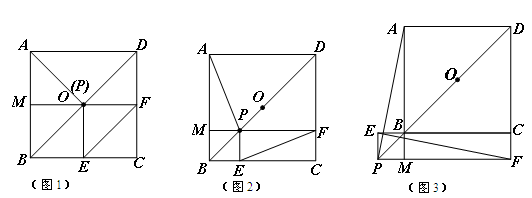
相关知识点
推荐套卷
正方形ABCD中,点O是对角线DB的中点,点P在DB所在的直线上,PE⊥BC于E,PF⊥DC于F.
(1)如图1,当点P与点O重合时,延长FP交AB于点M,求证:AP=EF;
(2)如图2,当点P在线段DB上(不与点D、O、B重合)时,延长FP交AB于点M,求证:AP=EF;
(3)如图3,当点P在DB的延长线上时,请你猜想AP与EF的数量关系及位置关系,直接写出结论;若不成立,请写出相应的结论.