随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: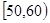 ,2;
,2;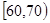 ,7;
,7;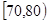 ,10;
,10;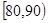 ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.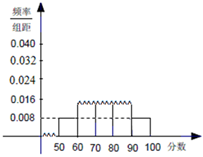
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中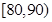 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为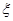 ,求
,求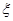 的数学期望.
的数学期望.
推荐套卷
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: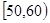 ,2;
,2;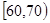 ,7;
,7;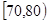 ,10;
,10;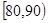 ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中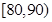 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为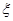 ,求
,求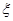 的数学期望.
的数学期望.