某校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如下图．
（1）求分数在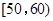
的频率及全班人数；
（2）求分数在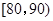
之间的频数，并计算频率分布直方图中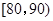间矩形的高；
（3）若要从分数在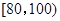
之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在
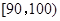之间的概率．
相关试题
的内角
的对边分别为
，
。
的大小；（2）若
，求
相切，
时，若不等式
总有解，求a的取值范围
是的前n项和为Sn，满足
中,内角
对边的边长分别是
.已知
.
,求
； 
,求
处的切线方程为12x＋y－1＝0．
上的最大值和最小值．推荐套卷
某校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如下图．
（1）求分数在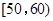的频率及全班人数；
（2）求分数在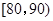之间的频数，并计算频率分布直方图中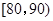间矩形的高；
（3）若要从分数在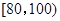之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在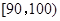之间的概率．
粤公网安备 44130202000953号