·大纲理)已知双曲线C: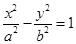 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、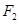 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为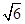 .
.
(1)求a,b;
(2)设过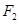 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且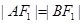 ,证明:
,证明: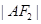 、
、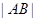 、
、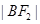 成等比数列.
成等比数列.
相关知识点
推荐套卷
·大纲理)已知双曲线C: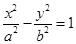 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、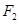 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为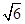 .
.
(1)求a,b;
(2)设过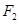 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且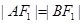 ,证明:
,证明: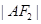 、
、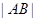 、
、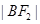 成等比数列.
成等比数列.