（（本题16分）
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃，要求同一区域上用同一种颜色鲜花，相邻区域用不同颜色鲜花，问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃，要求同一区域上用同一种颜色鲜花，相邻区域使用不同颜色鲜花．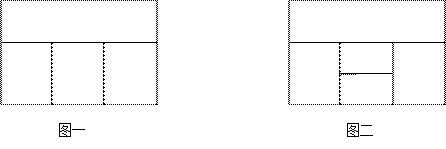
①求恰有两个区域用红色鲜花的概率；
②记花圃中红色鲜花区域的块数为S，求它的分布列及其数学期望E(S).
相关试题
，且
．
的解析式；
时，有
，求
的取值范围
＝
．
的值；
是R上的奇函数，且当
时，
在区间[1,3]上有最大值5和最小值2，求
的值
|
或
}，B＝{
或
}，若
，求实数
的取值范围．推荐套卷
（（本题16分）
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃，要求同一区域上用同一种颜色鲜花，相邻区域用不同颜色鲜花，问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃，要求同一区域上用同一种颜色鲜花，相邻区域使用不同颜色鲜花．
①求恰有两个区域用红色鲜花的概率；
②记花圃中红色鲜花区域的块数为S，求它的分布列及其数学期望E(S).
粤公网安备 44130202000953号