随着教育改革的不断深入，素质教育的全面推进，某市中学生利用假期参加社会实践活动的越来越多．王伟同学在本市丁牌公司实习时，计划发展部给了他一份实习作业：在下述条件下规划出下月的产量．假如公司生产部有工人200名，每个工人每2小时可生产一件丁牌产品，每个工人的月劳动时间不超过192小时，本月将剩余原料60吨，下个月准备购进300吨，每件丁牌产品需原料20千克．经市场调查，预计下个月市场对丁牌产品需求量为16000件，公司准备充分保证市场需求．请你和王伟同学一起规划出下个月产量范围．
如图，直线y=x+m和抛物线y=x2+bx+c都经过点A（1，0），B（3，2）．
（1）求m的值和抛物线的解析式；
（2）求不等式x2+bx+c＞x+m的解集．（直接写出答案）
△ABC在如图的平面直角坐标系中
（1）按要求画图：将△ABC向右平移3个单位长度后得△A1B1C1，再将△A1B1C1绕点O旋转180°后得到△A2B2C2．
（2）直接写出三角形A1A2B的面积．
如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC：BC＝4：3，点P从点A出发沿AB方向向点B运动，速度为1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为2cm/s，当一个动点到达终点时，另一个动点也随之停止运动．
（1）求AC、BC的长；
（2）设点P的运动时间为x（秒），△PBQ的面积为y（cm2），当△PBQ存在时，求y与x的函数关系式，并写出自变量x的取值范围；
（3）当点Q在CA上运动，使PQ⊥AB时，以点B、P、Q为定点的三角形与△ABC是否相似，请说明理由；
（4）当x=5秒时，在直线PQ上是否存在一点M，使△BCM得周长最小，若存在，求出最小周长，若不存在，请说明理由。
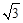，且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测角器的高度忽略不计）．
粤公网安备 44130202000953号