如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为3米，台阶AC的坡度为1：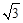
，且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测角器的高度忽略不计）．
，其中
＝
，
＝1。
的函数解析式为
，若抛物线
，请证明：
≥
,并说明
为何值时才会有
.
，设
用含有
的表达式表示出△
的面积
，并求出
的函数解析式。
，则
，
两点间的距离为）
相关知识点
推荐套卷
如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为3米，台阶AC的坡度为1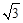：，且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测角器的高度忽略不计）．
粤公网安备 44130202000953号