如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,-a)(a、b均大于0);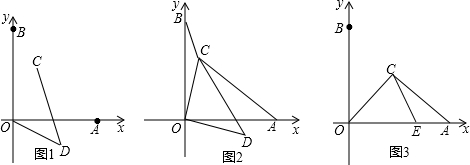
(1)连接OD、CD,求证:∠ODC=450;
(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;
(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求⊿OCA 的面积。
相关知识点
推荐套卷
如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,-a)(a、b均大于0);
(1)连接OD、CD,求证:∠ODC=450;
(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;
(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求⊿OCA 的面积。