（本小题满分15分）
已知椭圆C：＋＝1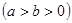
的离心率为，左焦点为F(－1，0)，
(1) 设A，B分别为椭圆的左、右顶点，过点F且斜率为k的直线L与椭圆C交于M，N两点，若
，求直线L的方程；
(2)椭圆C上是否存在三点P，E，G，使得S△OPE＝S△OPG＝S△OEG＝？
到
这
个，则任意两个数都不相邻的取法有多少种？
满足以下运算性质：
，
，求
为△
内的两点，且
=
+
=
的面积与△
的面积比
对任意的
都有
，设向量
，
，
，
，当
时，求
解集
与圆
:
交于
两点，若圆
的圆心在线段
上，且圆
上，求圆推荐套卷
（本小题满分15分）
已知椭圆C：＋＝1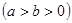的离心率为，左焦点为F(－1，0)，
(1) 设A，B分别为椭圆的左、右顶点，过点F且斜率为k的直线L与椭圆C交于M，N两点，若，求直线L的方程；
(2)椭圆C上是否存在三点P，E，G，使得S△OPE＝S△OPG＝S△OEG＝？
粤公网安备 44130202000953号