已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=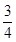 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4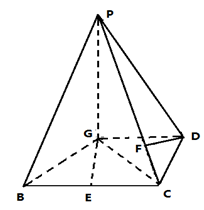
(1)求异面直线GE与PC所成角的余弦值;
(2)若F点是棱PC上一点,且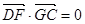 ,
,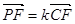 ,求
,求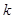 的值.
的值.
推荐套卷
已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=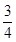 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
(1)求异面直线GE与PC所成角的余弦值;
(2)若F点是棱PC上一点,且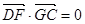 ,
,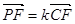 ,求
,求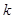 的值.
的值.