设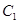 :
: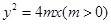 的准线与
的准线与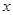 轴交于点
轴交于点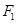 ,焦点为
,焦点为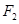 ;椭圆
;椭圆 以
以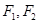 为焦点,离心率
为焦点,离心率 .设
.设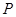 是
是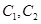 的一个交点.
的一个交点.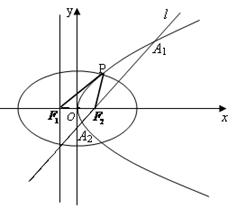
(1)当 时,求椭圆
时,求椭圆 的方程.
的方程.
(2)在(1)的条件下,直线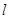 过
过 的右焦点
的右焦点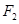 ,与
,与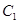 交于
交于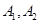 两点,且
两点,且 等于
等于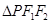 的周长,求
的周长,求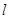 的方程.
的方程.
(3)求所有正实数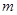 ,使得
,使得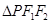 的边长是连续正整数.
的边长是连续正整数.
推荐套卷
设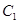 :
: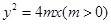 的准线与
的准线与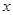 轴交于点
轴交于点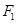 ,焦点为
,焦点为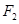 ;椭圆
;椭圆 以
以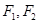 为焦点,离心率
为焦点,离心率 .设
.设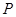 是
是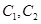 的一个交点.
的一个交点.
(1)当 时,求椭圆
时,求椭圆 的方程.
的方程.
(2)在(1)的条件下,直线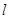 过
过 的右焦点
的右焦点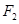 ,与
,与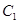 交于
交于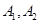 两点,且
两点,且 等于
等于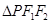 的周长,求
的周长,求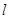 的方程.
的方程.
(3)求所有正实数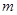 ,使得
,使得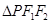 的边长是连续正整数.
的边长是连续正整数.