如图,已知平面内一动点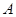 到两个定点
到两个定点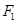 、
、 的距离之和为
的距离之和为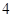 ,线段
,线段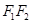 的长为
的长为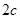
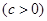 .
.
(1)求动点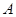 的轨迹
的轨迹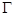 ;
;
(2)当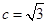 时,过点
时,过点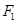 作直线
作直线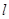 与轨迹
与轨迹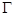 交于
交于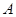 、
、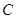 两点,且点
两点,且点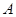 在线段
在线段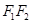 的上方,线段
的上方,线段 的垂直平分线为
的垂直平分线为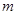
①求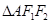 的面积的最大值;
的面积的最大值;
②轨迹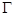 上是否存在除
上是否存在除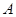 、
、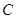 外的两点
外的两点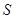 、
、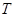 关于直线
关于直线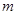 对称,请说明理由.
对称,请说明理由.
推荐套卷
如图,已知平面内一动点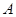 到两个定点
到两个定点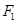 、
、 的距离之和为
的距离之和为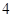 ,线段
,线段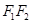 的长为
的长为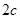
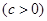 .
.
(1)求动点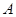 的轨迹
的轨迹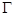 ;
;
(2)当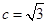 时,过点
时,过点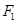 作直线
作直线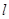 与轨迹
与轨迹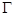 交于
交于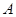 、
、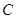 两点,且点
两点,且点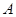 在线段
在线段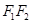 的上方,线段
的上方,线段 的垂直平分线为
的垂直平分线为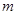
①求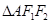 的面积的最大值;
的面积的最大值;
②轨迹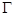 上是否存在除
上是否存在除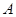 、
、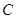 外的两点
外的两点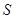 、
、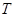 关于直线
关于直线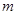 对称,请说明理由.
对称,请说明理由.