从数列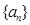 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列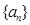 的一个子列.
的一个子列.
(1)写出数列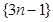 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)设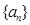 是无穷等比数列,首项
是无穷等比数列,首项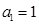 ,公比为
,公比为 .求证:当
.求证:当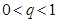 时,数列
时,数列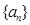 不存在
不存在
是无穷等差数列的子列.
相关知识点
推荐套卷
从数列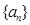 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列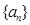 的一个子列.
的一个子列.
(1)写出数列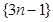 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)设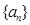 是无穷等比数列,首项
是无穷等比数列,首项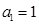 ,公比为
,公比为 .求证:当
.求证:当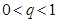 时,数列
时,数列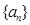 不存在
不存在
是无穷等差数列的子列.