如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.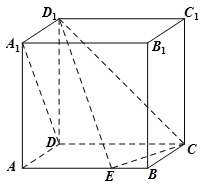
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45o,求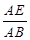 的值;
的值;
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).
相关知识点
推荐套卷
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45o,求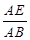 的值;
的值;
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).