如图,已知椭圆C的方程为 +y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
(1)设P是椭圆C上任意一点,若 =m
=m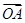 +n
+n ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两个动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的面积是否为定值,并说明理由.
推荐套卷
如图,已知椭圆C的方程为 +y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
(1)设P是椭圆C上任意一点,若 =m
=m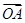 +n
+n ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两个动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的面积是否为定值,并说明理由.