已知椭圆C的两个焦点是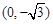
)和
，并且经过点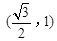
，抛物线的顶点E在坐标原点，焦点恰好是椭圆C的右顶点F．
（1）求椭圆C和抛物线E的标准方程；
（2）过点F作两条斜率都存在且互相垂直的直线l1、l2，l1交抛物线E于点A、B，l2交抛物线E于点G、H，求
的最小值．
的最大值为1．
的值；（2）求使
成立的x的取值集合．
，
，
，点
为坐标原点，点
是直线
上一点，求
的最小值及取得最小值时
的值．
；
；（2）求证：
．
、
、
三点在一条直线上，
，
，
，且
，求实数
，
的值．
，
，其中
．
；（2）求
的值．相关知识点
推荐套卷
已知椭圆C的两个焦点是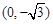)和，并且经过点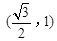，抛物线的顶点E在坐标原点，焦点恰好是椭圆C的右顶点F．
（1）求椭圆C和抛物线E的标准方程；
（2）过点F作两条斜率都存在且互相垂直的直线l1、l2，l1交抛物线E于点A、B，l2交抛物线E于点G、H，求的最小值．
粤公网安备 44130202000953号