已知三条直线
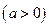 ,直线
,直线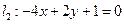 和直线
和直线 ,且
,且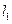 与
与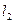 的距离是
的距离是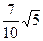
(1)求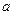 的值
的值
(2)能否找到一点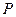 ,使得
,使得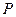 点同时满足下面三个条件,①
点同时满足下面三个条件,①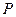 是第一象限的点;②
是第一象限的点;②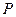 到
到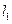 的距离是
的距离是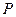 到
到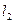 距离的
距离的 ,③
,③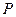 点到
点到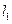 的距离与
的距离与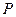 到
到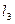 的距离之比是
的距离之比是 ,若能,
,若能, 求点
求点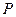 的坐标,若不能,说明理由。
的坐标,若不能,说明理由。
推荐套卷
已知三条直线
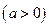 ,直线
,直线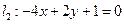 和直线
和直线 ,且
,且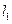 与
与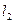 的距离是
的距离是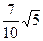
(1)求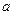 的值
的值
(2)能否找到一点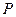 ,使得
,使得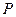 点同时满足下面三个条件,①
点同时满足下面三个条件,①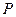 是第一象限的点;②
是第一象限的点;②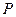 到
到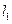 的距离是
的距离是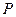 到
到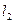 距离的
距离的 ,③
,③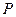 点到
点到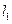 的距离与
的距离与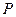 到
到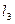 的距离之比是
的距离之比是 ,若能,
,若能, 求点
求点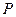 的坐标,若不能,说明理由。
的坐标,若不能,说明理由。