已知过曲线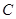 上任意一点
上任意一点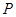 作直线
作直线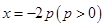 的垂线,垂足为
的垂线,垂足为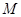 ,且
,且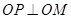 .
.
⑴求曲线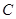 的方程;
的方程;
⑵设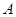 、
、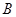 是曲线
是曲线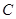 上两个不同点,直线
上两个不同点,直线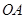 和
和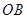 的倾斜角分别为
的倾斜角分别为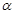 和
和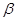 ,
,
当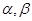 变化且
变化且 为定值
为定值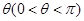 时,证明直线
时,证明直线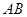 恒过定点,
恒过定点,
并求出该定点的坐标.
相关知识点
推荐套卷
已知过曲线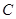 上任意一点
上任意一点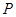 作直线
作直线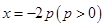 的垂线,垂足为
的垂线,垂足为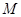 ,且
,且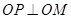 .
.
⑴求曲线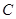 的方程;
的方程;
⑵设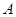 、
、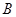 是曲线
是曲线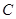 上两个不同点,直线
上两个不同点,直线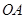 和
和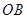 的倾斜角分别为
的倾斜角分别为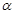 和
和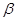 ,
,
当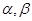 变化且
变化且 为定值
为定值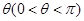 时,证明直线
时,证明直线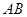 恒过定点,
恒过定点,
并求出该定点的坐标.