已知函数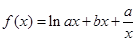 (
(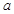 、
、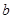 为常数),在
为常数),在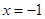 时取得极值.
时取得极值.
(1)求实数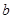 的取值范围;
的取值范围;
(2)当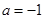 时,关于
时,关于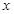 的方程
的方程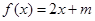 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数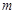 的取值范围;
的取值范围;
(3)数列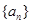 满足
满足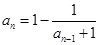 (
(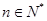 且
且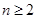 ),
),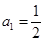 ,数列
,数列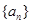 的前
的前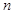 项和为
项和为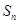 ,
,
求证: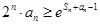 (
(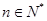 ,
,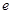 是自然对数的底).
是自然对数的底).
推荐套卷
已知函数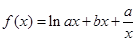 (
(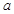 、
、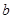 为常数),在
为常数),在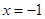 时取得极值.
时取得极值.
(1)求实数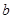 的取值范围;
的取值范围;
(2)当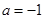 时,关于
时,关于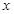 的方程
的方程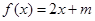 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数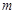 的取值范围;
的取值范围;
(3)数列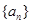 满足
满足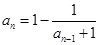 (
(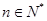 且
且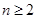 ),
),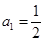 ,数列
,数列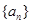 的前
的前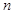 项和为
项和为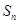 ,
,
求证: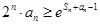 (
(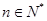 ,
,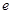 是自然对数的底).
是自然对数的底).