如图，在平面直角坐标系xOy中，椭圆C：
的离心率为
，短轴长是2．
（1）求a，b的值；
（2）设椭圆C的下顶点为D，过点D作两条互相垂直的直线l1，l2，这两条直线与椭圆C的另一个交点分别为M，N．设l1的斜率为k(k≠0)，△DMN的面积为S，当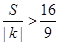
时，求k的取值范围．
，
。
；（2）求
的最大值及相应的
值；
中，已知
，
，
．
的值；（Ⅱ）求
的值
，若
，且
和
的值；（II）求
的值。
．
，n
，试求|m
n|的最小值．
顶点的分别为
，
，
，其中
．
，求
的值；（2）若
，求推荐套卷
如图，在平面直角坐标系xOy中，椭圆C：的离心率为，短轴长是2．
（1）求a，b的值；
（2）设椭圆C的下顶点为D，过点D作两条互相垂直的直线l1，l2，这两条直线与椭圆C的另一个交点分别为M，N．设l1的斜率为k(k≠0)，△DMN的面积为S，当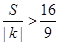时，求k的取值范围．
粤公网安备 44130202000953号