在三棱锥SABC中，底面是边长为2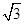
的正三角形，点S在底面ABC上的射影O恰是AC的中点，侧棱SB和底面成45°角．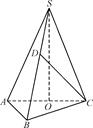
(1)若D为侧棱SB上一点，当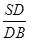
为何值时，CD⊥AB；
(2)求二面角S-BC-A的余弦值大小．
相关试题
的奇偶性并证明；
，证明：函数
在区间（2，
）上是增函数
，集合A=｛
，集合B＝
(2) (
)
(3) 
的函数
是奇函数.
的值.
在
恒成立, 求实数
的取值范围.
相关知识点
推荐套卷
在三棱锥SABC中，底面是边长为2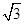的正三角形，点S在底面ABC上的射影O恰是AC的中点，侧棱SB和底面成45°角．
(1)若D为侧棱SB上一点，当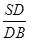为何值时，CD⊥AB；
(2)求二面角S-BC-A的余弦值大小．
粤公网安备 44130202000953号