已知f(n)＝1＋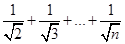
n∈N)，g(n)＝2(
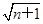－1)(n∈N)．
(1)当n＝1，2，3时，分别比较f(n)与g(n)的大小(直接给出结论)；
(2)由(1)猜想f(n)与g(n)的大小关系，并证明你的结论．
相关试题
中，
为
为
边上的动点.
；
，求三棱锥
的体积.
，设函数
的最小正周期及单调递增区间；
时，求
，
的前项和为
，已知
，
是
和
的等比中项。
对于任意
, 总有
，
，
上的单调递增函数
，求解不等式
相关知识点
推荐套卷
已知f(n)＝1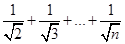＋n∈N)，g(n)＝2(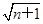－1)(n∈N)．
(1)当n＝1，2，3时，分别比较f(n)与g(n)的大小(直接给出结论)；
(2)由(1)猜想f(n)与g(n)的大小关系，并证明你的结论．
粤公网安备 44130202000953号