选修4－1：几何证明选讲
如图所示，已知⊙O1与⊙O2相交于A，B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1，⊙O2于点D，E，DE与AC相交于点P．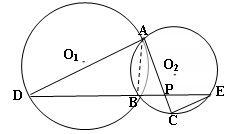
（1）求证：AD∥EC；
（2）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长；
，解不等式
.
，解不等式
.
|OB|,求椭圆的离心率.
，求椭圆的标准方程.推荐套卷
选修4－1：几何证明选讲
如图所示，已知⊙O1与⊙O2相交于A，B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1，⊙O2于点D，E，DE与AC相交于点P．
（1）求证：AD∥EC；
（2）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长；
粤公网安备 44130202000953号