如图,直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.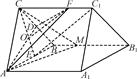
(1)求证:C1E∥平面ADF;
(2)设点M在棱BB1上,当BM为何值时,平面CAM⊥平面ADF?
推荐套卷
如图,直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(1)求证:C1E∥平面ADF;
(2)设点M在棱BB1上,当BM为何值时,平面CAM⊥平面ADF?