已知线段MN的两个端点M、N分别在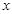
轴、
轴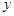上滑动，且
，点P在线段MN上，满足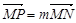
，记点P的轨迹为曲线W．
(1)求曲线W的方程，并讨论W的形状与
的值的关系；
(2)当
时，设A、B是曲线W与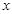轴、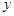轴的正半轴的交点，过原点的直线与曲线W交于C、D两点，其中C在第一象限，求四边形ACBD面积的最大值．
是等比数列；
是等差数列，
，求数列
的前n项和Sn.
中，
是其前
项和，
，求：
及
.推荐套卷
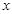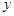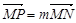
已知线段MN的两个端点M、N分别在轴、轴上滑动，且，点P在线段MN上，满足，记点P的轨迹为曲线W．
(1)求曲线W的方程，并讨论W的形状与的值的关系；
(2)当时，设A、B是曲线W与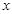轴、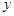轴的正半轴的交点，过原点的直线与曲线W交于C、D两点，其中C在第一象限，求四边形ACBD面积的最大值．
粤公网安备 44130202000953号